Methodologies

Ask the Survey Doctor: Finding Control Groups to Evaluate National Programs

By Craig Charney | Insights | Series II | No. 1 | December 2013

Q: How can we use control and comparison groups for evaluations in non-experimental situations involving countrywide programs or campaigns?

A: Good question – and a frequent problem. When programs call for big, national-scale programs, it is particularly difficult to separate out control or comparison groups from the “treatment” or “experimental” groups. After all, the treatment has been applied everywhere! But there are solutions…

One is prior research: pilot or experimental studies on a smaller scale before a program is scaled up. This type of work can more easily isolate and compare experimental and control groups that are selected to be similar in relevant aspects (economic, social, political, geographic, as the case may be). However, a variety of circumstances may prevent piloting – and even when pilots work, it is good to have confirmation that the program taken to scale is making a difference, too. How can this be done?

One way is to look for variations in exposure to the program to compare. Even when programs are national in scope, there often are differences in the extent to which members of the population are exposed to them. Surveys can be particularly helpful in disentangling these groups, which often may live in the same neighborhood or even the same household.

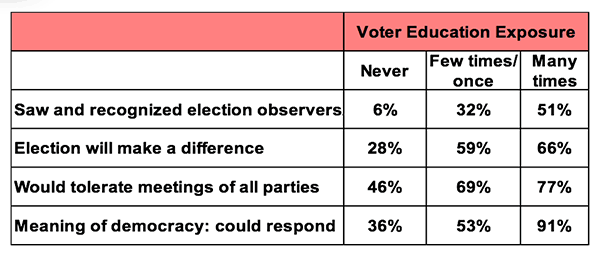
For example, when we evaluated USAID-funded voter education programs in Indonesia in 1999, after the country’s first democratic elections, we were able to group the members of the public by their self-reported exposure to the program. (See Fig. 1 below) We separated out those who were never exposed, who had seen materials once or a few times, and those who had seen the TV spots and publications many times. When we did, the results were dramatic: recognition of election observers, confidence in elections, democratic values and even knowing what democracy is were directly proportional to exposure to the program.

Fig 1: USAID supported TV spots had a measurable effect on attitudes to gender and politics.

Still, in a program like this, where there were a variety of interventions, how could you show that specific ones made a difference? We faced this problem in the voter education evaluation, because we wanted to find out whether specific USAID-funded efforts had made a difference – in particular, TV spots urging women to exercise their rights to become political leaders or to make their own voting choices without “help” from their menfolk. So here we tested for individuals’ exposure to specific program items – in this case, the individual spots – in the survey. (We did this by showing a still from the ad, reading the text, and asking if the respondent had seen it. Now, with tablets and smartphones much commoner, we would probably have the interviewer show the spot.)

Fig. 2: USAID supported TV spots had a measurable effect on attitudes to gender and politics.

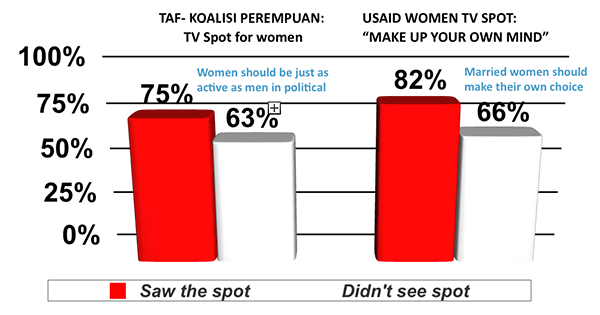
When we did this, we saw substantial differences between people exposed and not exposed — 12 points for the leadership spot, 16 points for the “own choice” ad. When you consider that 62 million people saw these spots, that works out to quite a difference. Pity it remains one of USAID’s best kept secrets!

But, a skeptic might say, maybe there’s another difference between your “exposed” and “control” groups that really accounts for their differing reactions, instead of the programs. Perhaps education? Educated people might be likelier to watch TV and to favor equality for women. How to test this?

If there’s just one additional factor, like education, you can control for it by cross-tabulating the data by both exposure AND educaton. If exposure makes a difference in the less- and better-educated groups, you show that the “third factor” doesn’t disprove the effect. On the other hand, if the difference between exposed and non-exposed vanishes when you control for education, then it cancels out the effect. (In the example above, it doesn’t.)

Say there are several potential “third factors” that might be at work, perhaps education, income, and urbanization, all of which might explain differences in both exposure to TV and attitudes to women’s rights. In that case, we would do multiple regression analysis, where we impose statistical controls to estimate the influence of each of them, as well as exposure to the program, on whatever the program is designed to influence. (For more detail, look in any statistics textbook.) This gives more precise estimates, but they are generally difficult for lay people to understand. You can also do regressions when there are just two variables involved, but unless you need the “betas” or regression coefficients, it’s usually easier for ordinary people to understand cross-tabulations.